随伴から作られるMonad

\gdef\Set{\mathrm{\mathbf{Set}}} \gdef\Hask{\mathrm{\mathbf{Hask}}} \gdef\Vect{\mathrm{\mathbf{Vect}}} \gdef\Mon{\mathrm{\mathbf{Mon}}} \gdef\id{\mathrm{id}} \gdef\Id{\mathrm{Id}} \gdef\map{\mathrm{map}} \gdef\op#1{{#1}^{\mathrm{\scriptsize op}}} \gdef\listof#1{\left\lbrack{#1}\right\rbrack}

前回の続きです。

Functor以外の関手を使って、次のモナドを分析していこうとしていました。

• Cont r (Control.Monad.Trans.Cont)
• ListT m (Control.Monad.Trans.List, “ListT done wrong”)

しかし、Functor以外の関手などというものをこれまできちんと定義してこなかったツケを返済するため、 前回は圏・関手・自然変換といった(数学の)用語の意味について、 Haskellでの例を引きながら説明しました。 今回はようやく本題に入れます。

Stateモナドの一般化に挑戦する

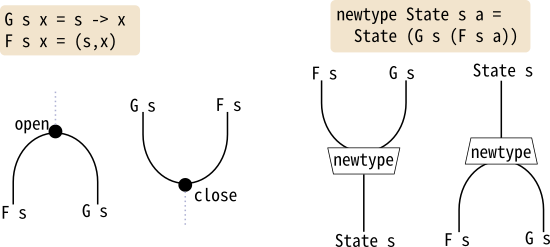
以前の記事では、 Stateモナドを以下の二つのFunctorの合成と考えることで、 きれいなストリング図が書けることを紹介しました。

-- G s = (s ->)も F s = (s, )もFunctor
type G s = (->) s
type F s = (,) s

newtype State s a = State { runState :: G s (F s a) }
  -- State s a ~ Compose (G s) (F s) a

open :: a -> G s (F s a)   -- a -> (s -> (s, a))
open a = \s -> (s, a)

close :: F s (G s a) -> a  -- (s, s -> a) -> a
close (s, f) = f s

ここで使った”トリック”は、 恒等関手Identityからふたつの関手の合成G s ∘ F sをつくる自然変換 openと、逆にF s ∘ G sからIdentityを取り出すcloseを考えるというものでした。

さて、モナドを合成関手と見て、特別な自然変換からモナド演算pure, joinを導くという手法は、 別の回でもやっています。 「二つのモナドmのnに対する分配swap :: ∀a. n (m a) -> m (n a)を見つけることで、 m∘nをモナドにする」という方法で、WriterTやReaderTを攻略しました。 では、open,closeを使う手法で作れるモナドはStateモナドのほかに無いのでしょうか？

実は、Stateモナドと同じ形のモナドしか作ることができないことが証明できます。 あるFとGがFunctorであり、自然変換open, closeを次のように持っていたとします。

-- 未知のF, GなるFunctor
instance Functor F
instance Functor G

-- 自然変換open, close
open :: a -> G (F a)
close :: F (G a) -> a

newtype M a = M { runM :: G (F a) }
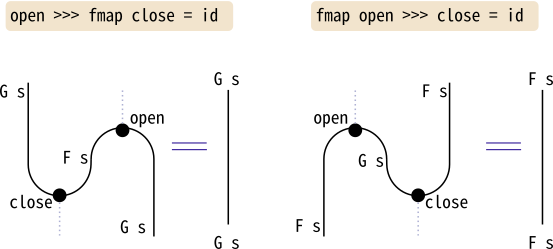
instance Monad M where -- etc.

そして、open, closeが上記ストリング図に書いた関係式を満たしているとします。 Haskellの式で書くなら、以下の等式になります。

open >>> fmap close = id :: G a -> G a
fmap open >>> close = id :: F a -> F a

このとき、任意の型xについて、G xがF () -> xと同型であり、 またF xが(F (), x)と同型であることが証明できてしまいます。 全部書き下すと長くなってしまうので概略だけ紹介します。

-- runG, makeGが同型の証拠になっている
runG :: G x -> (F () -> x)
runG gx f1 = close $ fmap (\() -> gx) f1
runG gx = fmap (\() -> gx) >>> close

makeG :: (F () -> x) -> G x
makeG fn = fmap fn (open ())

-- runG >>> makeG = id の計算だけ示す。
makeG (runG gx)
  = makeG (fmap (\() -> gx) >>> close)
  = fmap (fmap (\() -> gx) >>> close) (open ())
  = open >>> fmap (fmap (\() -> gx)) >>> fmap close $ ()
  -- openが自然変換 Identity ~> Compose G F であることを使う
  -- Identityについては、fmap f = Identity . f . runIdentity
  -- Compose G Fについては、fmap f = Compose . fmap (fmap f) . getCompose
  -- newtypeを無視すれば、open >>> fmap (fmap f) = f . open
  = (\() -> gx) >>> open >>> fmap close $ ()
  -- open >>> fmap close = id
  = (\() -> gx) $ ()
  = gx

結果的に、G (F x)はF () -> (F (), x)と同型、 すなわちState (F ()) xと同型になってしまい、 更にopen, closeから作ったモナド演算pure, joinもState (F ())のモナド演算と 同型の違いを除いて同じになってしまいます。 つまり、Stateモナドとは違うモナドは作れませんでした。

随伴

Stateモナドを作る材料となったFとGはFunctor、すなわち\Haskから\Haskへの関手でした。 これを任意の圏の間の関手に一般化すると、随伴とよばれるものになります。

圏Cから圏Dへの関手Fと、 圏Dから圏Cへの関手G（逆向き）について、 FがGの左随伴であるということを次のように定義します。

• 自然変換\mathrm{unit} \colon \Id_C \to G\circ Fが存在する。

  • \Id_Cは圏C上の恒等関手です。

  • 自然変換の定義を当てはめれば、すべてのCの対象aに対して定義された射の族 \mathrm{unit}_a \in C(\Id_C(a), G(F(a)))で、任意の射f\in C(a,b)に対して \mathrm{unit}_b \circ \map_{\Id_C}(f) = \map_{G\circ F}(f) \circ \mathrm{unit}_a を満たすもののことです。

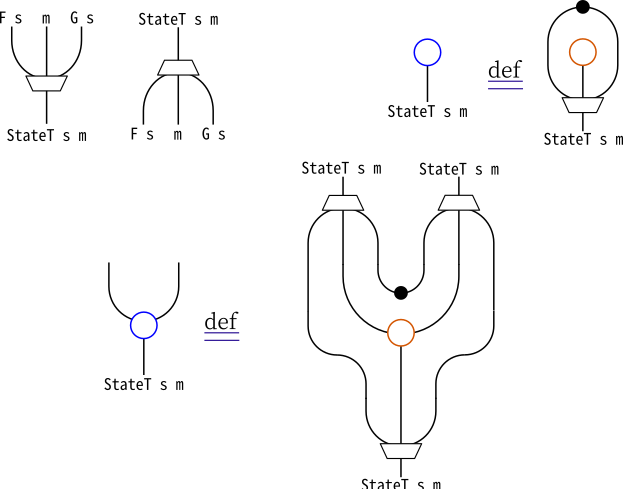
    恒等関手をわざわざ書かないことにすれば、\mathrm{unit}_a \in C(a, G(F(a)))となります。 openの型∀a. a -> G s (F s a)と見比べれば、\mathrm{unit}はopenの一般化として考えることができます。

• 自然変換\mathrm{counit} \colon F\circ G \to \Id_Dが存在する。

  • \Id_Dは圏D上の恒等関手です。

  • \mathrm{counit}はcloseの一般化として考えることができます。

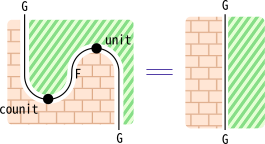
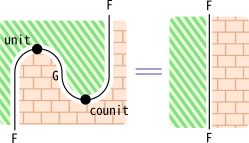
• \mathrm{unit}と\mathrm{counit}は、以下のジグザグ関係式を満たします。

  \begin{equation} \mathrm{counit}_{F(a)} \circ \map_F(\mathrm{unit}_a) = \id_{F(a)} \end{equation} \begin{equation} \map_G(\mathrm{counit}_a) \circ \mathrm{unit}_{G(a)} = \id_{G(a)} \end{equation}

ここで、C=\Haskである場合を考えます。すなわち、Fは\HaskからDへの関手、 GはDから\Haskへの関手です。このとき、G\circ Fは\Haskから\Haskへの関手で、 Stateと同じようにしてMonadになります。

\begin{equation} \mathrm{pure} = \mathrm{unit} \colon \forall a. a \to G(F(a)) \end{equation} \begin{equation} \mathrm{join} = \map_G(\mathrm{counit}) \colon \forall a. G(F(G(F(a)))) \to G(F(a)) \end{equation}

随伴をストリング図に描く

以前の記事で導入したストリング図は、 Functorすなわち\Haskから\Hask自身への関手と、それらの間の自然変換だけを考えていました。 ですが、その記事で説明したストリング図は、そのままでも任意の圏どうしの関手を扱うように拡張できます。

例えば、関手Fはストリング図では線で描かれます。 そして、Fが圏Cから圏Dへの関手であったなら、Fの線の左側の領域に「ここは圏Cである」、 右側の領域に「ここは圏Dである」と書き込むことで、この関手の型を明示することができます。

同じように、圏Dから圏Cへの関手Gも描けます。

（ここでは模様付きで領域に色を塗りましたが、別にそこまでする必要はありません。 わかり易さのためにラベル付けしているだけであって、無くてもかまわないものです。）

ストリング図に複数の関手の合成関手が出てきたとき、それは並行する線で表されていました。 合成関手G\circ Fは並行するFとGの線で表されており、 Fの右側の領域はGの左側の領域でもあるのですが、F,Gが合成できているため、 この領域に書き込まれる圏の名前は一致しているはずです。 なので、ひとつの領域には丁度ひとつの圏のラベルが書き込まれます。

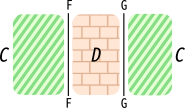
FがGの左随伴だとします。このとき、自然変換\mathrm{unit}, \mathrm{counit}は、 次のようにストリング図に描かれます。

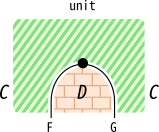
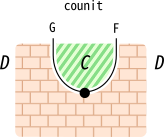
ジグザグ関係式も、以下のように描けます。

随伴からCont rを作る

State s以外のモナドで、随伴から作られているものの例として、 まずは継続モナドCont rについて考えます。

継続モナドCont rは、関手(_ -> r)を二つ合成したものと見ることができます。

newtype Cont r a = Cont { runCont :: (a -> r) -> r }
--      Cont r a ~ ((_ -> r) ∘ (_ -> r)) a

instance Monad (Cont r) where
  pure = pure' >>> Cont
  join = fmap runCont >>> runCont >>> join' >>> Cont

pure' :: a -> ((a -> r) -> r)
pure' a = \ar -> ar a

join' :: ((a -> r) -> r) -> r) -> r) -> ((a -> r) -> r)
join' arrrr
  = arrrr . pure'
  = \ar -> arrrr (pure' ar)
  = \ar -> arrrr (\arr -> arr ar)

ここで、(_ -> r)は、Contravariantすなわち\op\Haskから\Haskへの関手です。

-- 実際にはこのような記述はできない、疑似コードです
instance Contravariant (_ -> r) where
  contramap :: (a -> b) -> (b -> r) -> (a -> r)
  contramap f g = g . f

また、一般論として\op{C}からDへの関手は、 Cから\op{D}への関手と見なすこともできます¹。そのため、 (_ -> r)は\Haskから\op\Haskへの関手、かつ\op\Haskから\Haskへの関手です。

ですので、Cont rは（見た目は同じですが）二つの関手

• (_ -> r): \Haskから\op\Hask
• (_ -> r): \op\Haskから\Hask

を合成したCont r = (_ -> r) ∘ (_ -> r)として考えることができます。

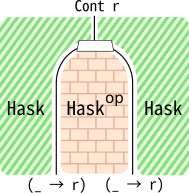
先程の一般論「関手Fが関手Gの左随伴なら、G\circ Fはモナドである」と、 Cont rがモナドであることを踏まえると、 「Cont rがモナドになるのは(_ -> r)が(_ -> r)の左随伴だったからなのでは！？」と予想できるでしょう。 実際のところ、それは正しいです。

type Hask = (->)
newtype Op a b = Op { getOp :: b -> a }

unit :: Hask a ((a -> r) -> r)
unit a = \k -> k a

counit :: Op ((a -> r) -> r) a
counit = Op unit

ジグザグ関係式も成り立っていますが、証明は省略します。

つまり、State sとCont rという、まったく異なるモナドが、 「随伴の関係にある関手の合成」として同じように理解できるのです。 嬉しいですね！

リストモナド[]を随伴に分ける

リストモナド[]も、随伴\listof{} = U\circ F, F \dashv Uに分けることが可能です。 ここで、Fは\Haskから「モノイドの圏」\Monへの関手、 Uは\Monから\Haskへの関手です。

「モノイドの圏」とは何か、F,Uはどんな関手なのか、 定義を書き下していきます。

• 「モノイドの圏」\Monを次のように定めます。

  • \Monの対象は、\Haskの対象である型aと、 その型aのMonoidのインスタンスを合わせたものです。

  • \Monの射f\in \Mon(a,b)は、関数f :: a -> bであって、 モノイド準同型であるものです。

    • Example: StringもSum IntもMonoidのインスタンスで、\Monの対象です。
    • Example: f = Sum . length :: String -> Sum Intはモノイド準同型で\Monの射です。
    • Non-example: g = const (Sum 5) :: String -> Sum Intはモノイド準同型ではないので、\Monの射ではありません。

• \Haskから\Monへの関手Fを、次のように定めます²。

  • \Haskの対象a、すなわち型aに対して、F(a)はaのリスト[a]です。

    任意の型aについてインスタンスMonoid [a]があるので、[a]は\Monの対象です。

  • \Haskの射f\in \Hask(a,b)、すなわち関数f :: a -> bに対して、 F(f)はmap f :: [a] -> [b]です。任意のfについてmap fはモノイド準同型になっており、 \Monの射の集合\Mon(F(a), F(b))に含まれます。

  • 「これはFunctor []とは何が違うのか？型aを[a]に写し、fmap = mapと言っているだけじゃないか！」 と考える人も居るかと思います。何が違うのかというと、[a]がモノイドであり、 mapがモノイド準同型であるという知識を、 「\Haskより限定的な圏\Monへの関手である」と表しているのです。 言うなれば、「実質的には同じだけれど、より”強い”型を付けている」と思ってください。

• \Monから\Haskへの関手Uを、次のように定めます³。

  • \Monの対象aは型なので、\Haskの対象でもあります。 U(a)は、\Monの対象aに対して、 それがMonoidのインスタンスを持っていることを忘れて、\Haskの対象と見なします。

  • \Monの射f \in \Mon(a,b)はモノイド準同型f :: a -> bでした。 U(f)は、これが準同型だったことを忘れて、単なる関数として\Haskの射と見なします。

そして、FはUの左随伴です。

• 自然変換\mathrm{unit}は、関数unit = (\a -> [a]) :: a -> [a]です。
• 自然変換\mathrm{counit}は、モノイド準同型counit = mconcat :: Monoid a => [a] -> aです⁴。

ジグザグ関係式を確かめてみましょう。 \Haskと\Monのどちらの圏なのかは（実際の対象と射は共通で、制限の有無しか違わないので） 雑に無視して計算すれば、以下のようになります。

\begin{equation} \begin{split} U(\mathrm{counit}) \circ \mathrm{unit} &= U(\mathrm{counit}) \circ (\lambda a. \listof{a}) \\ &= \mathrm{mconcat} \circ (\lambda a. \listof{a}) \\ &= \id_{\listof{a}} \end{split} \end{equation}

\begin{equation} \begin{split} \mathrm{counit} \circ F(\mathrm{unit}) &= \mathrm{counit} \circ \map(\mathrm{unit}) \\ &= \mathrm{mconcat} \circ \map (\lambda a. \listof{a}) \\ &= \id_{\listof{a}} \end{split} \end{equation}

この随伴によってU\circ FはMonadになります。 このMonadは通常のMonad []と全く同じものです。

ListT mは随伴のサンドイッチだった

前節では[]を随伴F\colon \Hask\to\MonとU\colon\Mon\to\Hask のペアとして表しましたが、これだけでは有用には見えません。そこで、 応用例を出してみましょう。

関手F\colon C\to Dに右随伴G\colon D\to Cがあれば、 G\circ F\colon C\to Cがモナドになるということを説明しました。 これは、自然変換open, closeを使ったStateモナドの構成の一般化だったのですが、 StateTモナド変換子もopen, closeを使って作れたことを思い出してください（過去記事）。

StateTモナド変換子は、関手F s = (s, _)と関手G s = (s -> _)の随伴があるとき、任意のモナドmに対して G s ∘ m ∘ F sもモナドになることを原理としていました。

同じことが任意の圏のあいだの随伴でも言えます。上記F,Gに対して、圏D上のモナドTがあれば、 StateTの場合とまったく同じようにしてG\circ T\circ F\colon C\to Cが圏C上のモナドになります。

これを、リストモナド[]をつくる随伴F\colon \Hask\to\Mon, U\colon\Mon\to\Haskに適用してみましょう。 つまり、\Mon上のモナドTに対して、G\circ T\circ Fというモナドが作れます。 このモナドは一体どういったものなんでしょうか？

\Mon上のモナドとは何か、というところから考えてみます。一般に圏C上のモナドTとは

1. 関手C\to Cであって
2. 自然変換\mathrm{pure}\colon \Id_C \to Tを持ち
3. 自然変換\mathrm{join}\colon T\circ T\to Tを持ち
4. \mathrm{pure}と\mathrm{join}がモナド則（右単位則、左単位則、結合則）を満たす

ものです。つまり、\Mon上のモナドTとは、以下のようなものです。

1. 関手\Mon\to\Monである、つまり

   1. 任意のモノイドaについてT aもモノイドで
   2. 任意のモノイド準同型f :: a -> bについてモノイド準同型map_T f :: T a -> T bがあって
   3. map_T id = id と map_T f . map_T g = map_T (f . g) を満たす

2. 自然変換\mathrm{pure}\colon \Id_{\Mon} \to Tを持つ、つまり

   1. 任意のモノイドaについてモノイド準同型pure :: a -> T aを持ち、
   2. map_T f . pure = pure . f を満たす

3. 自然変換\mathrm{join}\colon T\circ T\to Tを持つ、つまり

   1. 任意のモノイドaについてモノイド準同型join :: T (T a) -> T aを持ち、
   2. map_T f . join = join . map_T (map_T f) を満たす

4. (pure, join)がモナド則（右単位則、左単位則、結合則）を満たす

さて、モノイドの圏\Monは\Haskの対象と射を制限したものでした。 そのため、\Hask上のモナドすなわち普通のMonadから、 \Mon上のモナドにもなっているものを探すのは不自然ではないでしょう。

TをあるMonadだとします。任意のモノイドaに対して、 T aをモノイドにする方法があります。

instance Semigroup a => Semigroup (T a) where
  tx <> ty =
    do x <- tx
       y <- ty
       pure (x <> y)

instance Monoid a => Monoid (T a) where
  mempty = pure mempty

T aのモノイド演算が上記のものであると仮定し、 map_T = fmapと定義すれば、Tは\Monから\Monへの関手になります。

map_T :: (Monoid a, Monoid b) => (a -> b) -> T a -> T b
map_T = fmap

-- f :: a -> b がモノイド準同型であると仮定すると、
-- map_T f :: T a -> T b もモノイド準同型になる
map_T f (mempty :: T a)
 = map_T f (pure mempty)
 = pure (f mempty :: a)
 = pure (mempty :: b)    -- f はモノイド準同型
 = mempty :: T b

map_T f (tx <> ty)
 = fmap f $ do
     x <- tx
     y <- ty
     return (x <> y)
 = do x <- tx
      y <- ty
      return (f (x <> y))
 = do x <- tx
      y <- ty
      return (f x <> f y) -- f はモノイド準同型
 = do x' <- fmap f tx
      y' <- fmap f ty
      return (x' <> y')
 = map_T f tx <> map_T f ty

さらにpureとjoinを（\Hask上の）Monadから流用すれば、上記の条件のほとんどを満たせます。 すでにわかっている条件を打消し線で消します：

1. 関手\Mon\to\Monである、つまり

   1. 任意のモノイドaについてT aもモノイドで
   2. 任意のモノイド準同型f :: a -> bについてモノイド準同型map_T f :: T a -> T bがあって
   3. map_T id = id と map_T f . map_T g = map_T (f . g) を満たす

2. 自然変換\mathrm{pure}\colon \Id_{\Mon} \to Tを持つ、つまり

   1. 任意のモノイドaについてモノイド準同型pure :: a -> T aを持ち、
   2. map_T f . pure = pure . f を満たす

3. 自然変換\mathrm{join}\colon T\circ T\to Tを持つ、つまり

   1. 任意のモノイドaについてモノイド準同型join :: T (T a) -> T aを持ち、
   2. map_T f . join = join . map_T (map_T f) を満たす

4. (pure, join)がモナド則（右単位則、左単位則、結合則）を満たす

残っているもの、つまり\Mon上のモナド特有の条件はpureとjoinがモノイド準同型になることだけです。

pureとjoinがモノイド準同型になるためには、以下の4つの等式が成り立っている必要があります。

-- 1
pure mempty = mempty
-- 2
pure (x <> y) = pure x <> pure y
-- 3
join mempty = mempty
-- 4
join (ttx <> tty) = join ttx <> join tty
  where ttx, tty :: T (T a)

これらのうち、4番目の式以外は、任意のモナドTについて成り立っています(証明略)。 しかし、4番目のjoin (ttx <> tty) = join ttx <> join ttyはそうではありません。 例えば、TとしてIOモナドを選ぶと、この式は成り立ちません。

-- T=IOで4番目の式が成り立たない反例
ttx, tty :: IO (IO (Sum Int))
ttx = return (putStrLn "X" >> return (Sum 1))
tty = putStrLn "Y" >> return (return (Sum 2))

join ttx <> join tty
 = do x <- join ttx
      y <- join tty
      return (x <> y)
 = do x <- (putStrLn "X" >> return (Sum 1))
      y <- (putStrLn "Y" >> return (Sum 2))
      return (x <> y)
 = do putStrLn "X"
      putStrLn "Y"
      return (Sum 1 <> Sum 2)

join (ttx <> tty)
 = join $ do
     tx <- ttx
     ty <- tty
     return $ do
       x <- tx
       y <- ty
       return (x <> y)
 = do tx <- ttx
      ty <- tty
      x <- tx
      y <- ty
      return (x <> y)
 = do tx <- return (putStrLn "X" >> return (Sum 1))
      ty <- (putStrLn "Y" >> return (return (Sum 2)))
      x <- tx
      y <- ty
      return (x <> y)
 = do putStrLn "Y"
      putStrLn "X"
      return (Sum 1 <> Sum 2)

join (ttx <> tty)とjoin ttx <> join ttyでは出力の順番が違ってしまいます。 すなわち、joinがモノイド準同型ではありません。

この4番目の等式が成り立つことと、Tが可換なモナドであることは同値な条件になります。 （可換なモナドについては過去記事でも取り上げました。）

まとめると、以下のようになります。

1. \Mon上のモナドTがあれば、Monadすなわち\Hask上のモナドU\circ T\circ Fができる。
2. 可換なMonadであるTは、ここまで述べた方法で\Mon上のモナドにできる
3. したがって、可換なMonadであるTに対して、新しいMonadであるU\circ T\circ Fができる。

この新しいMonadは具体的にどんな形をしているでしょうか？ Fはただ、Functor []の行き先を\Monに制限したものでした。 Uは\Monの制限を忘れるだけでした。したがって、新しいモナドU\circ T \circ Fは以下のように実装できます。

-- T にあたるパラメータの名前は、モナド変換子の慣習にそってmとしました。
newtype ListT m a = ListT { runListT :: m [a] }
-- ListT m ~ m ∘ []

-- 「m は可換なモナドである」のクラス
class Monad m => CommutativeMonad m
  -- メソッドは一つも必要ないけれども、
  -- 可換なモナドに限ってこのクラスのインスタンスを
  -- 提供しなければならない！

instance (CommutativeMonad m) => Monad (ListT m) where
  pure a = ListT (pure [a])
  join = fmap runListT >>> runListT >>> join' >>> ListT

join' :: CommutativeMonad m => m [m [a]] -> m [a]
join' = join . fmap counit'

counit' :: (CommutativeMonad m, Monoid b) => [m b] -> m b
counit' = foldr (<<>>) (pure mempty)
  where mx <<>> my = do x <- mx; y <- my; return (x <> y)

これはそう、ListT (done wrong) に他なりません！

つまり、ListTは、ある意味では間違って(wrong)はいなかったのです。 （もちろん可換なモナドしか使えないというのは”モナド変換子としては”問題で、 そのためにListT done rightが作られたとも言えます。）