ストリング図でMonad再入門(1)

いまさらモナド

この記事はHaskellにおけるモナドの解説です。 そして、「またかよ」「もう知ってる」と思われた方が想定読者です。

（ほんとうにモナドについて初めて理解したくて来た方は申し訳ありません。 一応アドバイスするなら、私はHaskell Wiki等のWeb上の資料と すごいHaskell で学びました。基礎を抑える感じの良い本と思いましたが、 合わなかったという感想もよく聞きます。）

ねらいとしては、 ストリング図という表記法を使って、 モナドについての（おそらくすでに知っているでしょう）計算が とても視覚的にできるようになって楽しいということの紹介です。

以下の文献・Webページを参考にしました。

• String diagram - Wikipedia
  • ざっくりした概要
  • Wikipedia日本語版にはなかった（残念）
• 絵算の威力をお見せしよう - 檜山正幸のキマイラ飼育記 (はてなBlog)
  • 日本語、すごく勉強になるブログ
  • リンク先記事が最もまとまっていると感じましたが、それ以外にもたくさん参考にしました。
• Composing Monads, Mark P. Jones and Luc Duponcheel, Research Report YALEU/DCS/RR-1004, 1993
  • Monad transformersの原点的なもの
• 他たくさんあると思いますが、覚えてなくてリストアップできませんごめんなさい・・・

ストリング図

ストリング図は、 圏論で使われる表記法です。圏論から道具を拝借するときによくあることですが、 ストリング図は”2-圏における2-射”という抽象度の高いものを描くよう定義されています。 しかし、今回の記事の中では、Monadについて考えるだけなので、抽象度を下げたもの を説明していきます。

ストリング図が表すものは、Functorの間の自然変換です。 改めて明示的に定義するなら、 Functor fとFunctor gに対して、型∀a. f a -> g aが付くような関数が、fからgへの自然変換です。

ストリング図において、自然変換tf :: ∀a. f a -> g aは以下の図のように いくつかの線が上下に出ているノードとして表します。 ここで、自然変換は「上から下に」向いているものとして描きます。¹ 上側に出ている線が自然変換の引数側のFunctorであるfに、 下側に出ている線が返り値側のFunctorであるgに相当します。

“何もしない”自然変換id :: ∀a. f a -> f aはただの線で描きます。

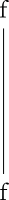
更に、∀a. f (g (h a)) -> p (q a)のようにFunctorがネストしているような場合も、 f (g (h a))とCompose f (Compose g h) aを、p (q a)とCompose p qを同一視して、Compose f (Compose g h)からCompose p qへの自然変換とみなすことにします。 何段ネストしていても同様に考え、更にComposeがどのような順で結合しているのかも特に気にしません。つまり、

• 以下のFunctorはどれも区別せず、3つの関手f, g, hがその順で合成されたものと考える
  • Compose f (Compose g h)
  • Compose (Compose f g) h
• 以下のFunctorはどれも区別せず、4つの関手f, g, h, kがその順で合成されたものと考える
  • Compose f (Compose g (Compose h k))
  • Compose (Compose f g) (Compose h k)
  • Compose (Compose (Compose f g) h) k
• ……任意の個数で同様……

となっています。

このようなネストしたFunctor間の自然変換は、下図のように描くことにします。²

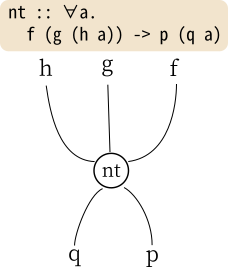
上に突き出している端が左からh, g, fなのは、この自然変換がFunctorの合成Compose f (Compose g h)を入力にとることを表していて、 下に突き出している端が左からq, pなのは、Compose p qを出力することを表しています。 合成がHaskellとは逆順なのに注意してください。

さらに、“0個のFunctorのネスト”をも、Identityと同一視します。 つまり、pure :: ∀a. a -> f aもIdentityからfへの自然変換とみなして、次の図のように書くことにします。このとき、図でうすく描いたような、Identityを表す線は引かないことにします。 （これによって後で困ることはありません！）

自然変換どうしは垂直合成する（“縦につなげる”）こともできました。上図のntとfooは、 合成して自然変換nt >>> foo :: ∀a. f (g (h a)) -> p aを作ることができます。 このように合成した自然変換は、 図を縦につなげて以下のように表します。 （ここでは、foo . ntのように.を使わず、代わりに>>>で関数の合成を表記することにします。）

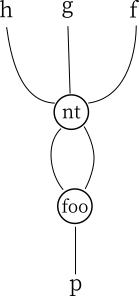
自然変換どうしを水平に合成する（“横にならべる”）こともできます。 ふたつの自然変換tf :: ∀a. f a -> f' a と tg :: ∀a. g a -> g' aがあるとき、tfg :: ∀a. f (g a) -> f' (g' a) が次のように定義できます。

tfg :: ∀ a. f (g a) -> f' (g' a)
tfg = fmap tg >>> tf
    = tf >>> fmap tg
  -- どちらも等しい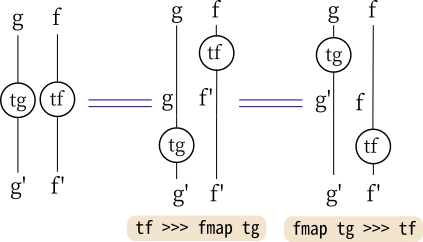

とくに、idと水平合成する場合が頻出です。

例を挙げてみましょう。次のように、catMaybesを maybeToListとconcatで表したとします。

catMaybes :: [Maybe a] -> [a]
catMaybes = fmap maybeToList >>> concat

concat :: [[a]] -> [a]
maybeToList :: Maybe a -> [a]

catMaybes, maybeToList, concatのいずれも、（ネストを許した広い意味で）自然変換です。 catMaybesの右辺をストリング図で描いてみると次のようになります。 Maybeと[]の合成順（左から右、Haskellでの記述と逆順）に気をつけてください。

ストリング図でMonad

Monadの定義を決めておきます。 ここでは、現実にHaskellで使われている定義ではないですが、 同値な定義として次のクラスをMonadだとします。

-- | Monadのインスタンスは以下のモナド則を満たさなければならない。
--
-- [単位法則]
--
--     > pure >>> join = fmap pure >>> join = id
--     普段どおり(.)を使って書くならば、
--     > join . pure   = join . fmap pure   = id
--
-- [結合法則]
--
--     > join >>> join = fmap join >>> join
--     普段どおり(.)を使って書くならば、
--     > join . join = join . fmap join
class (Functor m) => Monad m where
  pure :: a -> m a
  join :: m (m a) -> m a

return :: Monad m => a -> m a
return = pure

(>>=) :: Monad m => m a -> (a -> m b) -> m b
ma >>= f = join (fmap f ma)

pure、joinともに自然変換であり、モナド則も含めて ストリング図で描くことができます。 これにより、文字で書かれた「FunctorであるmがMonadである」という条件が、 次のように図で描けてしまいます。

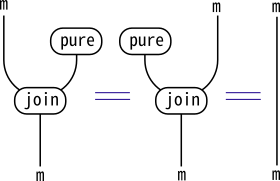
• 以下の自然変換pureとjoinがあること：

  

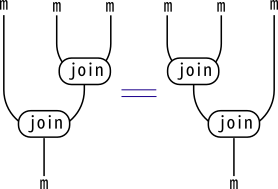
• 加えて、以下のストリング図の等式が成り立つこと：

  

  

ストリング図でStateモナド

次のStateモナドがモナド則を満たしていることを証明してみましょう。

newtype State s a = State { runState :: s -> (s, a) }

instance Functor (State s) where {- 省略 -}

instance Monad (State s) where
  pure a = State (\s -> (s, a))
  join mma = State $ \s ->
    let (s', ma) = runState mma s
    in runState ma s

ここで、Stateが二つのFunctorの合成からなっていることに注目して、 次のように書き換えてみます。

type G s = (->) s -- (s ->) と書きたいが、Haskellはこの書き方は不可
type F s = (,) s  -- (s, )  〃

-- G s = (s ->)も、 F s = (s, )も、Functorのインスタンス

newtype State s a = State { runState :: G s (F s a) }
  -- State s a ~ Compose (G s) (F s) a

instance Monad (State s) where
  pure = open >>> State
  join =   runState              -- :: State s (State s a) -> G s (F s (State s a))
       >>> fmap (fmap runState)  -- :: G s (F s (State s a)) -> G s (F s (G s (F s a)))
       >>> fmap close            -- :: G s (F s (G s (F s a))) -> G s (F s a)
       >>> State                 -- :: G s (F s a) -> State s a

open :: a -> G s (F s a)   -- a -> (s -> (s, a))
open a = \s -> (s, a)

close :: F s (G s a) -> a  -- (s, s -> a) -> a
close (s, f) = f s

openとcloseという命名は、これらが対になっているところからきています。

open >>> fmap close = id :: G s a -> G s a
(open >>> fmap close) (f :: G s a)   -- G s a = (s -> a)
  = fmap close $ \s -> (s, f)
  = \s -> close (s, f)
  = \s -> f s
  = f

fmap open >>> close = id :: F s a -> F s a
(fmap open >>> close) ((s, a) :: F s a)  -- F s a = (s, a)
  = close $ (s, open a)
  = close $ (s, \s -> (s, a))
  = (\s -> (s, a)) s
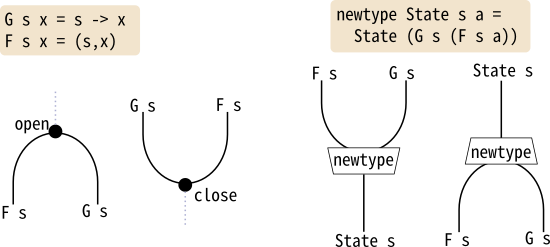
  = (s, a)

open, closeと、Stateのnewtypeをつけたり外したりするState, runStateはいずれも自然変換 になっており、以下の通りストリング図に描けます。

そして、openとcloseの間に成り立つ関係は次の図のように描けます。

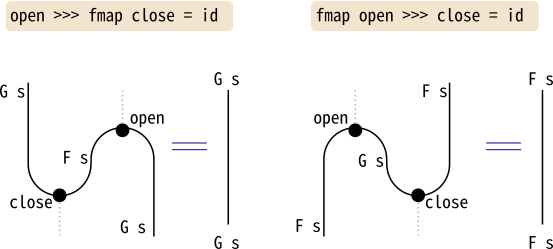
“曲がった線”をまっすぐに伸ばすことができるという、見た目にわかりやすい関係になっているところがポイントです。

ここまでの道具を使えば、Stateのモナド則は図を描いていくだけで証明できます。 まず、pureとjoinをストリング図で書きます。

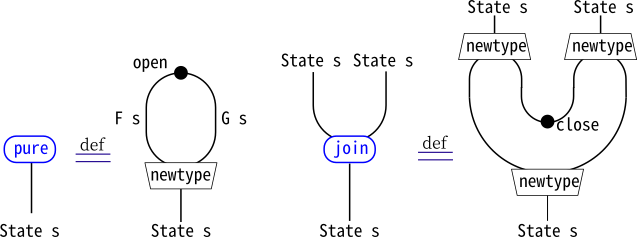
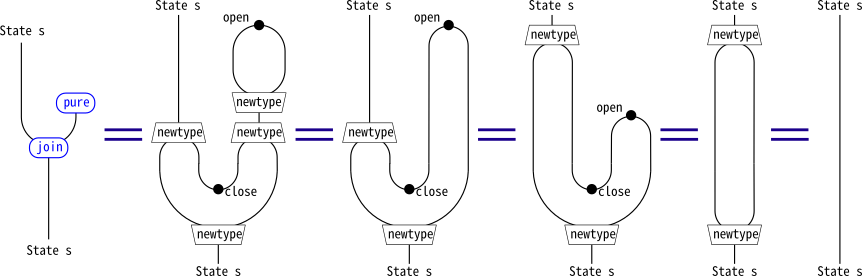
モナド則は、ストリング図の等式をつかって変形していくことで証明できます。

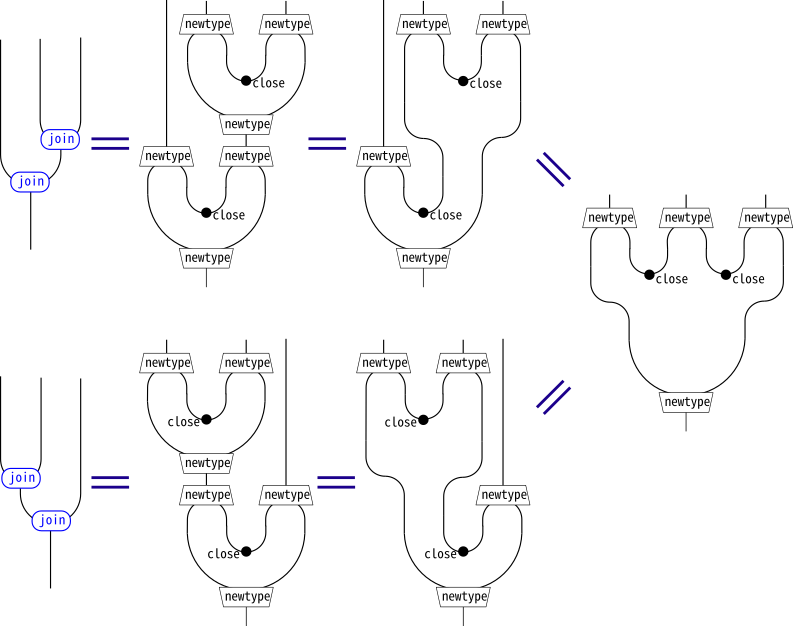
変更履歴

• 2025-04-10: “ストリング図(合成Functor2)”にあった誤りを修正 (Thanks: @Kory__3 (tweet)), ほか説明を書き直す