前回、
ストリング図について紹介しました。
例として、ストリング図を使ってモナド則を視覚的に表して、
Stateモナドのモナド則をストリング図の変形で証明しています。
しかし、Stateモナドのような単純なケースでは、ストリング図のありがたみが
まだわからないかもしれません。
今回は、StateTモナド変換子(Control.Monad.Trans.State.Lazyを参照)のモナド則を、
ストリング図で示してみます。
(あと、ちょっときれいな図を描けるようになりました。)
ストリング図でStateT
前回の記事で使ったStateモナドの定義を再掲します。
(証明を楽にするために、Monadクラスの定義もHaskell標準のものからちょっと変えています。)
type G s = (->) s -- (s ->) と書きたいが、Haskellはこの書き方は不可
type F s = (,) s -- (s, ) 〃
newtype State s a = State { runState :: G s (F s a) }
-- State s a ~ Compose (G s) (F s) a
instance Monad (State s) where
pure = open >>> State
join = runState -- :: State s (State s a) -> G s (F s (State s a))
>>> fmap (fmap runState) -- :: G s (F s (State s a)) -> G s (F s (G s (F s a)))
>>> fmap close -- :: G s (F s (G s (F s a))) -> G s (F s a)
>>> State -- :: G s (F s a) -> State s a
open :: a -> G s (F s a) -- a -> (s -> (s, a))
open a = \s -> (s, a)
close :: F s (G s a) -> a -- (s, s -> a) -> a
close (s, f) = f sこの流儀に沿って、StateTを定義し直してみます。
嬉しいことに、Stateモナドの定義からopenとcloseを流用できます。
newtype StateT s m a = State { runState :: G s (m (F s a)) }
-- StateT s m a ~ (G s `Compose` m `Compose` F s) a
-- ~ s -> m (s, a)
instance Monad m => Monad (StateT s m) where
pure = open -- a -> G s (F s a)
>>> fmap pure -- G s (F s a) -> G s (m (F s a))
>>> StateT -- G s (m (F s a)) -> StateT s m a
join = fmap runState -- :: StateT s m (StateT s m a) -> StateT s m (G s (m (F s a)))
>>> runState -- :: StateT s m (G s (m (F s a))) -> G s (m (F s (G s (m (F s a)))))
>>> fmap (fmap close) -- :: G s (m (m (F s a)))
>>> fmap join -- :: G s (m (F s a))
>>> StateT -- :: G s (m (F s a)) -> StateT s m aちょっと複雑になってしまいましたが、ストリング図にこれらの定義を起こしてみましょう。

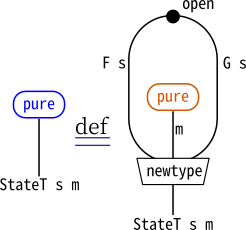
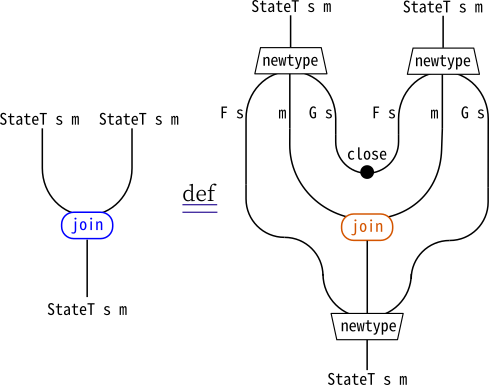
図の中で、変換されるモナドmのpureやjoinと、
これから構成するStateT s mのpureやjoinは、色をつけて区別しています。
さて、図が煩雑になってきたので、以降はラベルを省いて描いてしまいます。

特に、モナドのpure,joinは、どちらもラベルのない丸記号○だけで済ますことにします。
つながっている線の本数が違うため、pureとjoinの区別をつけるのに困ることはないです。
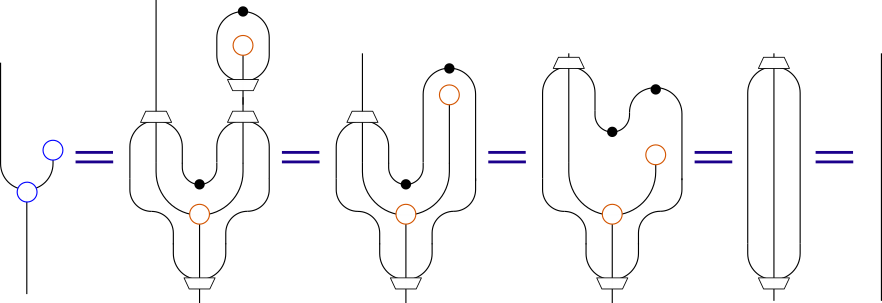
この省略記法を使って、StateTのモナドの定義を描き直すと、次のようになります。
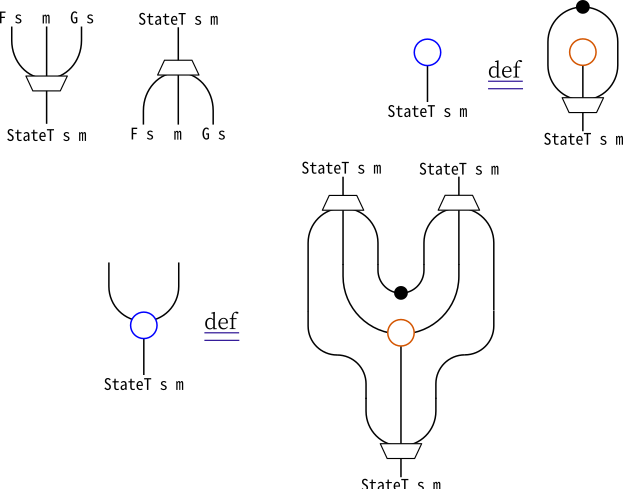
StateTのモナド則
StateT s mのモナド則も、Stateモナド同様に、
図をどんどん変形するだけでできてしまいます。
ここで、モナドmがもつpureとjoin(オレンジの丸)は、
モナド則を満たしていることが前提にできます。
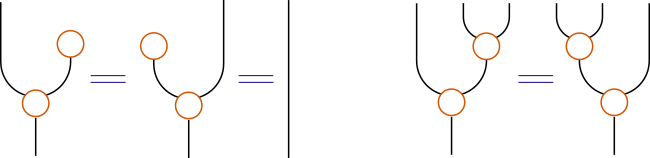
また、前回の記事同様、openとcloseの関係も使います。
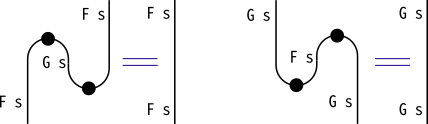
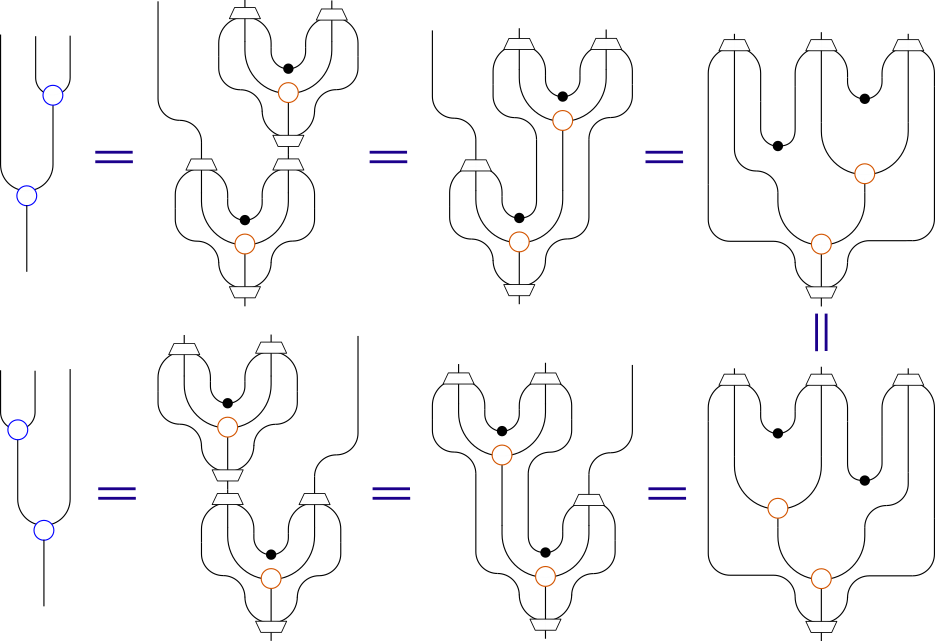
これらの変形を組み合わせれば、StateT s mのモナド則も、
図を描いてそれを変形させていくことで証明できます。
他のモナド変換子は?
ここまで来ると、ReaderTやWriterT、ExceptTといった、他のモナド変換子たちの
モナド則がどう証明できるかが気になるかと思います。
実のところ、StateTのモナド則というのは、
ストリング図による証明が一番簡単なたぐいのモナド変換子でした。
ReaderTやWriterTが成り立っている事情を説明するには、もうひとつ道具が必要です。
次の記事でそれを解説するつもりです。乞うご期待。