前回、ストリング図を使ってStateTモナド変換子のモナド則を証明しました。
今度はReaderT,WriterT,ExceptTの3つについてやっていきます。
共通の構造
前回の記事までは、証明の方針は私が天下り的に与えていましたが、 今回は「発見的な」やり方で説明してみようと思います。
WriterTの場合
まずは、WriterTの実装を眺めてみます。
-- transformers パッケージのものとは(同型ですが)少し違います
newtype WriterT w m a = WriterT { runWriterT :: m (w, a) }
instance Functor m => Functor (WriterT w m) where {- 省略 -}
instance (Monoid w, Monad m) => Monad (WriterT w m) where
pure = pureWriter >>> pure >>> WriterT
where
pureWriter :: Monoid w => a -> (w, a)
pureWriter a = (mempty, a) -- Writerモナド (w,_) のpure
join = fmap runWriterT >>> runWriterT >>> joinT >>> WriterT
where
joinT :: (Monad m, Monoid w) => m (w, m (w, a)) -> m (w, a)
joinT mwmwa =
do (w, mwa) <- mwmwa
(w', a) <- mwa
return (w <> w', a)ここで、pureは自然変換pureWriter, pure, WriterTの合成で書くことができていて、
ストリング図に書きやすそうです。
一方、joinの実装に使ったjoinTは、もっと単純な自然変換の合成で書けてはいないようです。
joinTをうまいこと自然変換たちに分解してみましょう。
-- Writerモナド(w,_)のjoinが使えそうです
joinWriter :: Monoid w => (w, (w, a)) -> (w, a)
joinWriter (w, (w', a)) = (w <> w', a)
joinT :: (Monad m, Monoid w) => m (w, m (w, a)) -> m (w, a)
joinT = \mwmwa -> do
(w, mwa) <- mwmwa
(w', a) <- mwa
return (w <> w', a)
= \mwmwa -> do
(w, mwa) <- mwmwa
fmap (\(w',a) -> (w <> w', a)) m
= \mwmwa -> mwmwa >>= \(w,mwa) -> mwa >>= \(w',a) -> return (w <> w', a)
= \mwmwa -> mwmwa >>= \(w,mwa) -> fmap (\(w',a) -> (w<>w',a)) mwa
= fmap (\(w,mwa) -> fmap (\(w',a) -> (w<>w', a)) mwa) >>> join
-- ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
-- ここで、この関数に注目してみます。
-- この関数の型は (w, m (w, a)) -> m (w, a) です。
-- また、関数の中身がjoinWriterに似ていますが、
-- そのままではjoinWriterで置き換えられる部分がありません。
--
-- なのでまず (w, m (w, a)) の外側のWriterモナドとmを入れ替え、
-- fmap joinWriter :: m (w, (w, a)) -> m (w, a) と合成するとよさそうです。
= fmap (swapWM >>> fmap joinWriter) >>> join
= fmap swapWM >>> fmap (fmap joinWriter) >>> join
where swapWM :: Functor m => (w, m b) -> m (w, b)
swapWM (w, mb) = fmap (\b -> (w,b)) mbめでたく、WriterTのjoinも単純な自然変換の合成で書けました。まとめると、
-- Writerモナド (w, )のpureとjoin
pureWriter :: Monoid w => a -> (w, a)
pureWriter a = (mempty, a)
joinWriter :: Monoid w => (w, (w, a)) -> (w, a)
joinWriter (w, (w', a)) = (w <> w', a)
-- Writerとmの入れ替え
swapWM :: Functor m => (w, m b) -> m (w, b)
swapWM (w, mb) = fmap (\b -> (w,b)) mb
instance (Monoid w, Monad m) => Monad (WriterT w m) where
pure = pureWriter >>> pure >>> WriterT
join = fmap runWriterT -- WriterT w m (WriterT w m a) -> WriterT w m (m (w, a))
>>> runWriterT -- WriterT w m (m (w, a)) -> m (w, m (w, a))
>>> fmap swapWM -- m (w, m (w, a)) -> m (m (w, (w, a)))
>>> fmap (fmap joinWriter) -- m (m (w, (w, a))) -> m (m (w, a))
>>> join -- m (m (w, a)) -> m (w, a)
>>> WriterT -- m (w, a) -> WriterT w m aこれをストリング図に描いてみます。

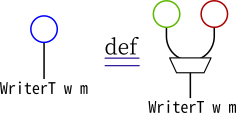
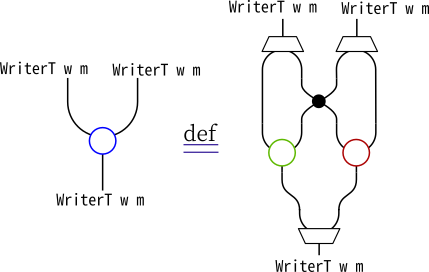
青丸をWriterT w mのモナド演算(pureまたはjoin)に当てていて、
同様に緑丸をWriterモナド、赤丸をモナドmに対応させています。
また、二つの線が交わるところにある点がswapWMです。
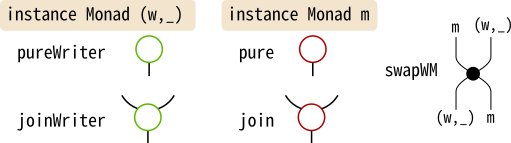
さて、私達はWriterTを構成する2つのモナド(w,_)とmのモナド演算については
よくわかっていますが、自然変換swapWMについてはよくわかっていません。
そのため、ひとまずWriterTのモナド則の証明は後回しにしておきます。
ReaderTの場合
ReaderTモナド変換子をストリング図に描く方法を考えます。
newtype ReaderT r m a = ReaderT { runReaderT :: r -> m a }
instance Functor m => Functor (ReaderT r m) where {- 省略 -}
-- WriterTはWriterモナドを部品として作ることができました。
-- ReaderTもそうなって欲しいですね。
pureReader :: a -> (r -> a)
pureReader = const
joinReader :: (r -> r -> a) -> (r -> a)
joinReader f r = f r r
instance (Monad m) => Monad (ReaderT r m) where
pure = pure >>> pureReader >>> ReaderT
join = fmap runReaderT >>> runReaderT >>> joinT >>> ReaderT
where
joinT :: (Monad m) => (r -> m (r -> m a)) -> r -> m a
joinT rmrma = \r -> rmrma r >>= \rma -> rma rふたたび、joinTが単純な自然変換の合成になっていませんが、
WriterTのときと同じ作戦でいってみましょう。
WriterT w mがWriter w = (w, )とmの合成Functorだったように、
ReaderT r mもmとReader r = (r -> _)の合成Functorです。
そのため、joinTの引数はFunctorの4段重ねr -> m (r -> (m _))になっています。
4段重ねの中央の2段、m (r -> _)を入れ替えられれば、Readerとmのjoinを使えます。
-- mとReaderの入れ替え
swapMR :: (Functor m) => m (r -> b) -> r -> m b
swapMR mrb r = fmap ($ r) mrb
-- swapMRで中央を入れ替える方針で型を合わせるパズルをすれば、
-- joinTと同じ型の自然変換が見つかります。
joinT' :: (Monad m) => (r -> m (r -> m a)) -> r -> m a
joinT' = fmap swapMR >>> fmap (fmap join) >>> joinReader
-- joinT' = joinT を確認します。
joinT' rmrma
= joinReader $ fmap (fmap join) $ fmap swapMR rmrma
= joinReader $ fmap (fmap join) $ \r -> swapMR (rmrma r)
= joinReader $ fmap (fmap join) $ \r r' -> fmap ($ r') (rmrma r)
= joinReader $ \r r' -> join $ fmap ($ r') (rmrma r)
= \r -> join $ fmap ($ r) (rmrma r)
= \r -> rmrma r >>= ($ r)
= \r -> rmrma r >>= \rma -> rma r
= joinT rmrmaこれをもとにストリング図を描くと、WriterTのものとラベル以外同じものが出来上がります。
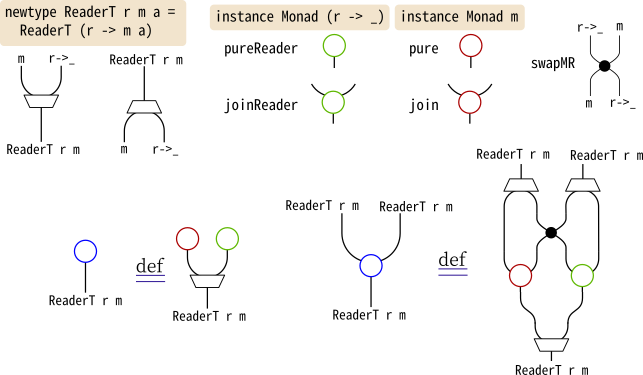
ExceptTの場合
ExceptTもReaderTやWriterTと”同じ構造”を持っています。
もはや細かい説明は不要かと思いますが、ExceptT e mはモナドmとモナドEither eの合成Functorで、
入れ替えをする自然変換swapEMによってモナドにしています。
newtype ExceptT e m a =
ExceptT { runExceptT :: m (Either e a) }
swapEM :: Monad m => Either e (m b) -> m (Either e b)
swapEM (Left e) = pure (Left e)
swapEM (Right mb) = fmap Right mb3つをひとまとめにする
WriterT、ReaderT、ExceptTはどれも、
モナドの合成順を入れ替える自然変換を使って定義できました。
この3つのどれも、以下の構造を持っています。
あるモナド
mとモナドnの合成m ∘ nになっている入れ替えをする自然変換
swap ::∀a. n (m a) -> m (n a)を持っているswapを使って、pureとjoinが下図のように定義されている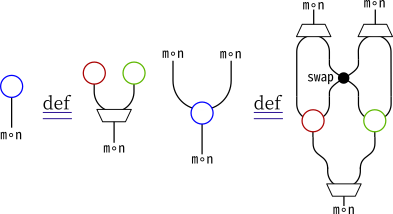
| モナド変換子 | 外側のモナド | 内側のモナド | swap |
|---|---|---|---|
WriterT w m |
m |
(w,_) |
swapWM :: (w, m b) -> m (w, b) |
ReaderT r m |
r -> _ |
m |
swapMR :: m (r -> b) -> r -> m b |
ExceptT e m |
m |
Either e |
swapEM :: Either e (m b) -> m (Either e b) |
モナドの合成のモナド則
任意のモナドの組み合わせm, nと前節のswapによって、
m ∘ nがモナドになると言いたいところですが、どんな自然変換でもよいのでしょうか?そんなことは無さそうです。
実際、なんでもOKではありません。WriterTの構成にあるswapWM :: (w, m a) -> m (w, a)で、
モノイドwを勝手にmemptyに置き換えたりすれば、
出来上がったWriterT w mはモナド則を満たさなくなってしまいます。
しかし、「swapが特定の条件を満たせばm ∘ nがモナドになる」とは言えるはずです。
ストリング図を描いて、どんな条件を満たせばよいのか考えてみます。
まず、左単位法則から見てみます。
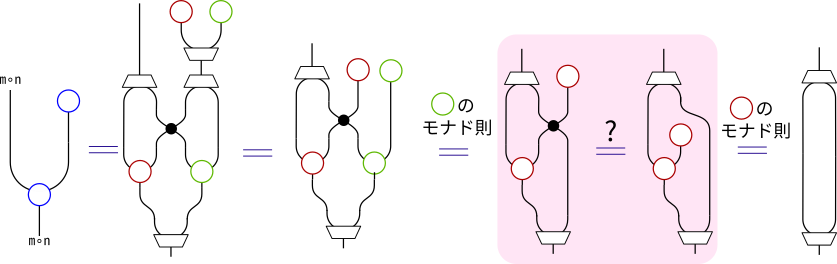
ピンク色で強調した部分が成り立っているかどうかわからない等式で、
それ以外の部分はm,nのモナド則といった、すでに知っている等式です。
この成り立ってほしい等式(1)は、もっと単純なバージョン(下図右辺)と同値になります。
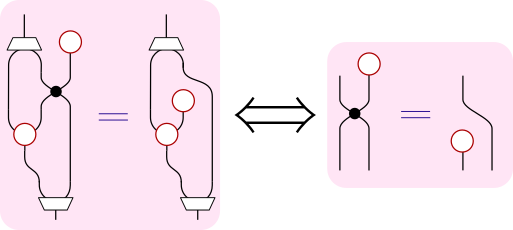
右単位法則が成り立つ条件から、同様に次の成り立ってほしい等式(2)が出てきます。
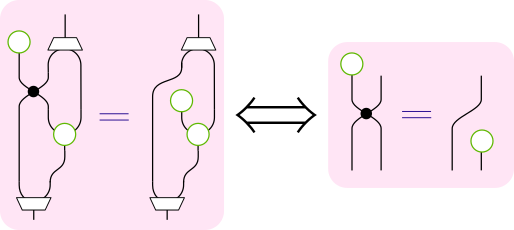
最後に結合法則を見てみます。(結合法則が成り立つために成り立ってほしい等式を、 ピンク色で強調しています。)
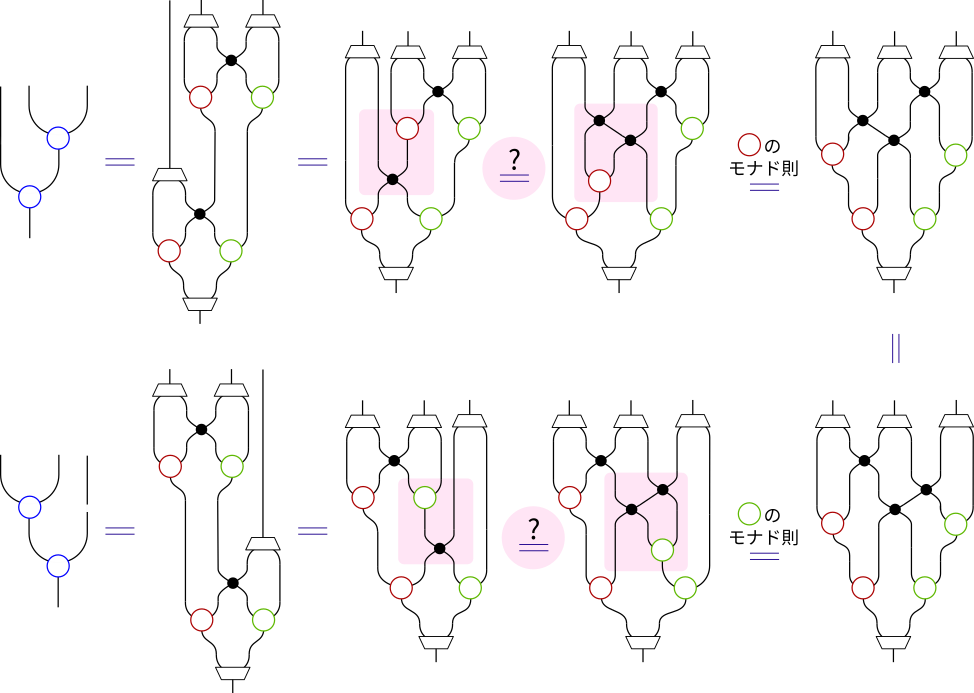
成り立ってほしい等式だけ取り出せば、次のようになります。
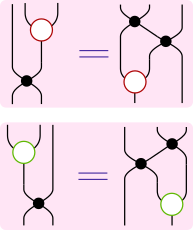
これらの等式(1)-(4)を満たすようなswapであれば、m ∘ nがモナドになると言えます。
等式(1)-(4)を、ストリング図からHaskellの式に書き直すと、次のようになります。
instance Monad m
instance Monad n
swap :: ∀b. n (m b) -> m (n b)
-- 等式(1)
pure >>> swap = fmap pure :: ∀b. m b -> m (n b)
-- 等式(2)
fmap pure >>> swap = pure :: ∀b. n b -> m (n b)
-- 等式(3)
join >>> swap :: ∀b. n (n (m b)) -> m (n b)
= fmap swap >>> swap >>> fmap join
-- 等式(4)
fmap join >>> swap :: ∀b. n (m (m b)) -> m (n b)
= swap >>> fmap swap >>> join自然変換swapによって(1)-(4)が成り立つことを、
「swapは、モナドmがモナドnに対する1分配である2」と呼ぶことにして、
ここで証明できたことをまとめると、次のようになります。
モナド
mがモナドnに対する分配swapを持てば、swapを使ってm ∘ nがモナドになる
これをWriterTの場合に適用すれば、WriterT w mがモナド則を満たしていることの証明は、
swap=swapWMが分配であることを確認すればOKです。
-- 再掲
swapWM :: Functor m => (w, m b) -> m (w, b)
swapWM (w, mb) = fmap (\b -> (w,b)) mb
-- 等式(1)
pureWriter >>> swapWM = fmap pureWriter :: ∀b. m b -> m (w, b)
(pureWriter >>> swapWM) mb
= swapWM (mempty, mb)
= fmap (\b -> (mempty, b)) mb
= fmap pureWriter mb
-- 等式(2)
fmap pure >>> swapWM = pure :: ∀b. (w, b) -> m (w, b)
fmap pure >>> swapWM $ (w,b)
= swapWM (w, pure b)
= fmap (\b -> (w,b)) (pure b)
= pure (w,b)
-- 等式(3)
joinWriter >>> swapWM :: ∀b. (w, (w, m b)) -> m (w, b)
= fmap swapWM >>> swapWM >>> fmap joinWriter
joinWriter >>> swapWM $ (w,(w',mb))
= swapWM (w <> w', mb)
= fmap (\b -> (w <> w', b)) mb
fmap swapWM >>> swapWM >>> fmap joinWriter $ (w,(w',mb))
= swapWM >>> fmap joinWriter $ (w, swapWM (w', mb))
= fmap joinWriter $ swapWM (w, swapWM (w', mb))
= fmap joinWriter $ fmap (\b -> (w,b)) $ fmap (\b -> (w',b)) mb
= fmap (joinWriter . (\b -> (w,b)) . (\b -> (w',b))) $ mb
= fmap (\b -> joinWriter (w,(w',b))) mb
= fmap (\b -> (w <> w', b)) mb
-- 等式(4)
fmap join >>> swapWM :: ∀b. (w, m (m b)) -> m (w, b)
= swapWM >>> fmap swapWM >>> join
fmap join >>> swapWM $ (w, mmb)
= swapWM (w, join mmb)
= fmap (\b -> (w,b)) $ join mmb
swapWM >>> fmap swapWM >>> join $ (w, mmb)
= fmap swapWM >>> join $ fmap (\mb -> (w,mb)) mmb
= join $ fmap (swapWM . (\mb -> (w,mb))) mmb
= join $ fmap (\mb -> swapWM (w,mb)) mmb
= join $ fmap (\mb -> fmap (\b -> (w,b)) mb) mmb
= join $ fmap (fmap (\b -> (w,b))) mmb
-- join . fmap (fmap f) = fmap f . join
= fmap (\b -> (w,b)) $ join mmbReaderTもExceptTも、同じようにswapMR、swapEMが分配であることが示せて、
モナド則を満たすことがわかります。
(注意)
「モナド
mがモナドnに対する……」において、mとnの順番には意味があります。swap :: ∀b. n (m b) -> m (n b)があるからといって、逆向きの自然変換reverseSwap :: ∀b. m (n b) -> n (m b)があったり、 それが等式(1)-(4)を満たす保証はまったく無いからです。そのため、「モナド
m,nの……」のように並列で呼ばないようにしました。↩︎「分配」という単語は、これが圏論では「分配律(distributive law)」と呼ばれていることから取っています。
「分配律」から「律」を落としたのは、モナド則の結合法則などの自然変換の間の等式と混同しないためです。 等式(1)-(4)を満たすような
swapそれ自体が「分配律」と呼ばれていて、等式(1)-(4)は「分配律」 の満たすべき性質(言うなれば「分配律律」)です。ややこしすぎて本文に書くことでは無いと思いました。↩︎