Cosemigroupについて

\gdef\Set{\mathrm{\mathbf{Set}}} \gdef\id{\mathrm{id}} \gdef\assoc{\mathrm{assoc}} \gdef\comult{\mathrm{comult}} \gdef\comp{\circ} \gdef\setbraces#1{\left\{{#1}\right\}} \gdef\blank{-}

Cosemigroup: Semigroupの双対

この記事では、半群(Semigroup)の双対と考えられる、Cosemigroupという概念について考えていきます。

Cosemigroupのアイデアと定義

Haskellでの半群の定義は以下のようになっていました。 （半群およびモノイドについては既知とします。）

class Semigroup a where
    -- | Semigroup則: @(<>)@ は以下の結合法則を満たす
    --
    -- @
    -- x <> (y <> z) == (x <> y) <> z
    -- @
    (<>) :: a -> a -> a

Semigroupの「双対をとったもの」は、2個のa型の値から1個のa型の値を作る<>という演算に対して、 1個の値から2個の値を取り出すcomultという演算を持ち、「結合法則」も流れを逆にした条件（余結合法則と呼ぶ）を持ちます。

つまり、次のようなクラスです。

-- | Cosemigroup則: @comult@は以下の余結合法則を満たす
--
-- @
-- first comult . comult = assoc . second comult . comult
-- @
class Cosemigroup a where
    comult :: a -> (a,a)

ここで、first, second, assocは次のように定義されているものとします。

first  f (a,b) = (f a, b)
second f (a,b) = (a, f b)
assoc (a,(b,c)) = ((a,b),c)

これがなぜ「結合法則」の逆であるのかは、データの流れを図にしてみると一目瞭然です。

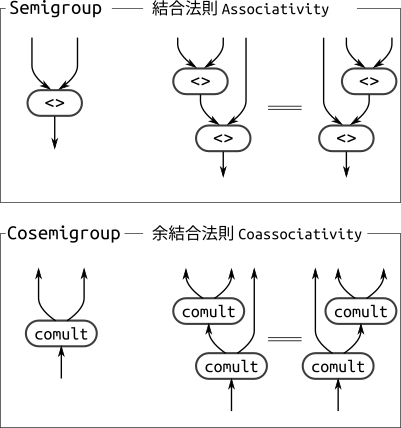
以降はHaskellでの表現を離れて、単に数学的なものとしてのCosemigroupを考えます。 更に言えば、 「集合と、その集合の上の演算と、演算の満たす公理」という形でCosemigroupを考えます¹。

次のように集合C上のCosemigroupを定義します。

Cosemigroupの定義（やや煩雑）

集合CがCosemigroupであるとは、Cについて関数\comult\colon C \to C \times Cが定義されていて、 \begin{equation} \left( \comult \times \id \right) \comp \comult = \assoc \comp \left( \id \times \comult \right) \comp \comult \end{equation} が成り立つことであると定義する。

ですが、この定義では直積集合を操作するためだけに\assocなどの関数が出てきて、煩雑になってしまいます。 そこで、 \comult(x) = \left(x\cdot l, x\cdot r \right)となるような2項演算(\blank \cdot \blank) \colon C \times \setbraces{l,r} \to Cを代わりに用いることにします。

Cosemigroupの定義

2つの異なる元からなる集合\setbraces{l,r}をとって固定する。集合CがCosemigroupであることを、2項演算(\blank \cdot \blank) \colon C \times \setbraces{l,r} \to Cがあり、3つの等式 \begin{align} (x \cdot l) \cdot l = x \cdot l \\ (x \cdot r) \cdot r = x \cdot r \\ (x \cdot l) \cdot r = (x \cdot r) \cdot l \end{align} が任意のx\in Cについて成り立つことであると定義する。

これは、\comultの余結合法則を(\blank \cdot l), (\blank \cdot r)を使って言い換えたものになっています。

• (\blank \cdot l)と(\blank \cdot r)は両方ともC上のべき等関数です。
• (\blank \cdot l)と(\blank \cdot r)はC上の関数として可換です。つまり、どの順で適用しても同じ結果になります。

これは更に、次のように言い換えられます。生成元\setbraces{l,r}と関係式\{l \cdot l = l, r \cdot r = r, l \cdot r = r \cdot l\}によって表示されるモノイドMを考えます。 このモノイドの元はl,rに単位元の1とl \cdot rを加えた²4つのみになります。以降、Mの元はM = \setbraces{1, l, r, l\cdot r}と書くことにします。

CがCosemigroupであることは、CがMによる作用³をもつことと同値になります。

Cosemigroupの定義（M-作用版）

Mを上記のモノイドとする。集合CがCosemigroupであることを、CがM-集合であること、 すなわちMの作用をもつことと定義する。

更に具体的に言えば、CがCosemigroupであれば、2項演算(\blank \cdot \blank) \colon C \times M \to Cがあり、 Cの元xとMの元a,bに対して、以下が成り立ちます。 \begin{align*} (x \cdot 1) &= 1\\ (x \cdot a) \cdot b &= x \cdot (a \cdot b) \end{align*}

ただし、記号(\blank \cdot \blank)を、モノイドMの間の積とCへの作用の両方に使いました。 また、以降はCの元xとMの元a,bについて、括弧を省略してx \cdot a \cdot bのように書くことにします。

Cosemigroupの例

HaskellでいうMaybe Aのように、集合Aに対してAに含まれない一点\starを付け加えた集合A + \setbraces{\star}は、 以下の3つの方法でCosemigroupにすることができます。

1. 任意のxに対して、x \cdot l = x \cdot r = \star
2. 任意のxに対して、x \cdot l = \star, x \cdot r = x
3. 任意のxに対して、x \cdot l = x, x \cdot r = \star

CosemigroupはM-集合のことであるため、モノイド作用を持つ集合の一般論から、 以下のような例が考えられます。

• 自明なCosemigroup

  任意の集合Xは、自明な作用によってM-集合になります。つまり、任意のa\in Mに対してx \cdot a = xと定義してCosemigroupにすることができます。

• Cosemigroupの直和

  2つの集合X, YがそれぞれCosemigroupになっているとします。

  XとXの集合としての直和X + Y上、もとの集合に対するMの作用をそのまま適用するように定義して、 X+YをCosemigroupにできます。特に断らなければ、単にX+Yと書いたとき、このCosemigroupを意味することにします。

  任意の集合Iで添字付けられたCosemigroupの族(X_i)_{i \in I}に対して、 IにわたるX_iの直和をとった集合(\sum_{i\in I} X_i)も、同様にしてCosemigroupになります。

• 空Cosemigroup

  \emptyset \times Mは空集合なので、 空関数\emptyset \times M \to \emptysetも\emptysetに対するM-作用と考えることができます。

• Cosemigroupの直積

  2つのCosemigroup X,Yに対して、直積集合X\times Yも以下のようにCosemigroupにすることができます。

  \begin{align*} (x,y) \cdot a &= (x \cdot a, y \cdot a) \end{align*}

弱推移的なCosemigroup

前節で見たCosemigroupの例にもあったように、Cosemigroupの中には「2つのCosemigroupの直和」 として表すことができるものもあります。 空でないCosemigroupCのうち、「2つの空でないCosemigroupの直和」 として表すことができないようなものは、l\cdot rを作用させることで1点に潰れてしまうようなCosemigroupです。 そのようなものを「弱推移的なCosemigroup」と呼ぶことにします⁴。

定義

Cosemigroup Cが弱推移的なCosemigroupである ⇔ C \cdot l\cdot r = \setbraces{c \cdot l\cdot r \mid c \in C}が1元集合

ただし、記法の簡便のために、Cosemigroup Cの部分集合X \subseteq Cに対してX \cdot aと書くと、 それぞれ集合の各要素にa作用させた集合を意味することにしました。

（弱推移的ならば直和ではない）

弱推移的なCosemigroupは2つの空でないCosemigroupの直和ではない。

どのCosemigroupも、弱推移的なCosemigroupの和として表されます。

（弱推移的成分への分解）

どんなCosemigroupCも、0個以上の弱推移的なCosemigroupの直和として表すことができる。

弱推移的なCosemigroupの表示

Cを任意のCosemigroupとします。このとき、Cを「C \cdot lに含まれるかどうか」および「C \cdot rに含まれるかどうか」という2つの基準で、 交わらない4つの集合I, L, R, Sに分割することを考えます。

\begin{align*} & I = C\cdot l \cap C\cdot r\\ & L = C\cdot l \setminus C\cdot r = C\cdot l \setminus I\\ & R = C\cdot r \setminus C\cdot l = C\cdot r \setminus I\\ & S = C \setminus (C\cdot l \cup C\cdot r) = C \setminus (L + R + I) \end{align*}

ここで、C\cdot l \cap C\cdot r = C\cdot l\cdot rなので⁵、弱推移的なCosemigroupにおいてIは1元集合になります。

Cが弱推移的なCosemigroupである場合に、上記の分割を考えます。Cが弱推移的であるため、Iは1元集合になりますが、その元をiと書くことにします。 すなわち、I=\setbraces{i}です。

この分割C = \setbraces{i} + L + R + Sに対して、l, rは次のように作用します。

\begin{align*} x \cdot l &= \begin{cases} i & \text{if} & x \in \setbraces{i} \\ x & \text{if} & x \in L \\ i & \text{if} & x \in R \\ f_L(x) & \text{if} & x \in S \end{cases}\\ x \cdot r &= \begin{cases} i & \text{if} & x \in \setbraces{i} \\ i & \text{if} & x \in L \\ x & \text{if} & x \in R \\ f_R(x) & \text{if} & x \in S \end{cases}\\ \end{align*}

ここで、f_Lは(\blank \cdot l)の定義域をSに、値域をC \cdot l = L+\setbraces{i}に制限した関数S \to L + \setbraces{i}であり、 f_Rも同様に(\blank \cdot r)の定義域をSに、値域をC \cdot r = R+\setbraces{i}に制限した関数S \to R + \setbraces{i}です。

逆に、任意の非空集合CがC = \setbraces{i} + L + R + Sと分割されていて、 関数f_L \colon S \to L + \setbraces{i}とf_R \colon S \to R + \setbraces{i}が与えられていれば、 上記のように(\blank \cdot l)と(\blank \cdot r)を定義して、Cは弱推移的なCosemigroupになります。

有限なCosemigroupの数え上げ

ここまででわかったこと、つまり

• Cosemigroupは、連結なCosemigroupの直和である
• 連結なCosemigroup Cは、C = \setbraces{i} + L + R + Sという分割と、2つの関数 f_L \colon S \to L + \setbraces{i}とf_R \colon S \to R + \setbraces{i}によって表される

ことを用いて、有限集合上の Cosemigroup の同型類を数えることに挑戦しました。

まず、連結なCosemigroupを考えてみます。|C| \le 3までの連結なCosemigroupは、以下のようにリスト化できます。

• |C| = 1のとき、あり得る連結なCosemigroupの数は1つ

• |C| = 2のとき、あり得る連結なCosemigroupの数は3つ

  分割された各集合の大きさを|S| = N, |L| = A, |R| = Bとおく。

  |C|	N	A	B	同型類の数
  2	1	0	0	1
  2	0	1	0	1
  2	0	0	1	1

• |C| = 3のとき、あり得る連結なCosemigroupの数は8つ

  分割された各集合の大きさを|S| = N, |L| = A, |R| = Bとおく。

  |C|	N	A	B	同型類の数
  3	2	0	0	1
  3	1	1	0	2
  3	1	0	1	2
  3	0	2	0	1
  3	0	1	1	1
  3	0	0	2	1

したがって、要素数3の集合上にあり得るCosemigroupは

• 直和1 + 1 + 1に分解されるケース： 1 \times 1 \times 1 = 1通り
• 直和2 + 1に分解されるケース: 3 \times 1 = 3通り
• 分解されないケース: 8通り

の合計12通りだとわかります。

ですが、集合のサイズが大きい場合、上記の表を作るために必要な「与えられた大きさのN,A,Bを持つ同型類の数」を求めることは難しそうでした。 f_L \colon S \to L + \setbraces{i}とf_R \colon S \to R + \setbraces{i}の組をすべて列挙すると(A+1)^N \times (B+1)^N個の関数の組が得られますが、 それらの中には同型なCosemigroupを定めるものもあります。

この数え上げは、次の問題と同等になります。

非負整数A,B,Nが与えられる。非負整数からなる(A+1) \times (B+1)行列で、全要素の合計がNになるもののうち、 「 1行目と1列目を動かさないような 行と列の並び替えで移り合う行列は等しい」という同一視の下で異なるものの数はいくつか？

例:

(A,B,N)=(1,0,2)のとき、非自明な行と列の並び替えはなく、要素の合計が2である2\times 1行列、すなわち

\begin{pmatrix} 2 \\ 0 \end{pmatrix}, \begin{pmatrix} 1 \\ 1 \end{pmatrix}, \begin{pmatrix} 0 \\ 2 \end{pmatrix}

の3個になる。

(A,B,N)=(2,2,1)のとき、つぎの4パターンになる。（3行目あるいは3列目に唯一の1がくるケースは、行と列の入れ替えで2行目または2列目になる）

\begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}

(A,B,N)=(2,2,2)のとき、17パターンになる。

\begin{align*} & \begin{pmatrix} 1 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 2 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 2 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \\ & \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 & 0 \\ 2 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \\ & \begin{pmatrix} 0 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} \end{align*}

この問題は、私の知識ではお手上げでした。

（この記事をアップロードする直前になってから解決の糸口は見つかったのですが、 まだ明確に理解しきれていないので本記事では「難しそう」としておきます！）

CosemigroupがHaskellにおいてどう重要なのか？

このCosemigroupというもの、Haskellにおいてなんの役に立つのでしょうか？ 正直なことを言うと私には思いつかないのですが、Cosemigroupを考えるとApplicativeについての知識が深まります。

「pureの無いApplicative」である、Applyという型クラスがあります。 以下にApplyの定義を引用します。

class Functor f => Apply f where
    (<!>) :: f (a -> b) -> f a -> f b

いま、「ある型Cからの関数(->) C」と同型な関手Fを考えます。

data C
newtype F a = F (C -> a)

instance Functor F where
    fmap f (F ca) = F (f . ca)

instance Apply F where
    F cab <!> F ca = {- ...... -}

Fに対して可能なあらゆる(<!>)の実装は、どれもC -> (C,C)という型の関数と一対一に対応します。

comultToApply :: (C -> (C,C)) -> F (a -> b) -> F a -> F b
comultToApply comult' (F cab) (F ca) = F (\c -> case comult c of (cl, cr) -> (cab cl) (ca cr))

applyToComult :: (forall a b. F (a -> b) -> F a -> F b) -> C -> (C,C)
applyToComult apply =
    let pass = F (id :: C -> C)
        F comult' = fmap (,) pass `apply` pass
     in comult'

更に、FがApply則を満たすことと、CがCosemigroup則を満たすことは、 上記の対応のもとで同値になります。

すなわち、Cosemigroupは、F a = C -> aという形をした関手の、あらゆるApplyのインスタンスを説明しているのです！

更に、より馴染み深いApplicativeに対しても、近いことが言えます。 以下の形をした関手Gを考えます。

data G a = One a | Fn (C -> a)

instance Functor G where
    fmap f (One a) = One (f a)
    fmap f (Fn ca) = Fn (f . ca)

ここで更に、GがApplicativeのインスタンスを持ち、pure = Oneであるとします。

instance Applicative G where
    pure = One
    (<*>) = {- ...... -}

このとき、<*>の定義としてありえるケースのうち、 Fn _ <*> Fn _以外はApplicative則から以下のように決まります。

One x <*> y = fmap x y
Fn cx <*> One y = Fn (\c -> cx c y)
Fn cx <*> Fn cy = {- ...... -}

更に、一部の例外を除いて、Fn cx <*> Fn cyの右辺は必ずFn _という形になります。 このとき、Applyに対して行ったのと同様にして、 Applicative Gとしてあり得る全てのインスタンスのうちpure = Oneであるものは、Cosemigroup Cのあり得るインスタンスと1対1に対応します。

Fn cx <*> Fn cy = One (cx c1 (cy c2))

x = Fn const      :: G (() -> C)
y = Fn (const id) :: G (() -> ())
z = Fn (const ()) :: G ()

x <*> (y <*> z)
  = x <*> (Fn (const id) <*> Fn id)
  = x <*> One (const id c1 (const () c2))
  = x <*> One ()
  = Fn const <*> One ()
  = Fn id
(.) <*> x <*> y <*> z
  = Fn ((.) . const) <*> Fn (const id) <*> z
  = One (((.) . const) c1 (const id c2)) <*> z
  = One ((.) (const c1) id) <*> z
  = One (const c1 . id) <*> z
  = One (const c1) <*> Fn (const ())
  = Fn (const c1)