Too lazy to evaluate

LambdaBoxの概要

まずはHello worldをご覧ください。

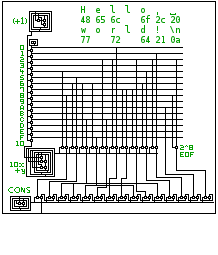
見ての通り、LambdaBoxのプログラムは画像です。この画像には白(#FFFFFF)・黒(#000000)・緑の3色が使われていますが、プログラムとして意味を持つのは「黒(#000000)か、そうでないか」だけです。それ以外の色の違いは無視されます。（緑色は、これを利用して「コメント」を書き込むために使っています。）

どのようにLambdaBoxのプログラムを書く（描く？）のかは、LanguageGuide.mdにまとめまてありますが、つたない英語で書いてありますし、ここでも説明していこうと思います。

中間言語

LambdaBoxは、まずラムダ計算をもとにした中間言語に翻訳され、その中間言語を実行するという形で定義されています。その中間言語は、次のような文法で定義されます：

<Expression> := <VarName>                                     # 変数
              | "(" <Expression> ")"
              | <Expression> <Expression>                     # 関数適用
              | "\" <ArgList> "->" <Expression>               # 関数抽象
              | "letrec" "{" <DefList> "}" "in" <Expression>  # letrec

<ArgList> := <VarName>
           | <VarName> <ArgList>

<DefList> := ε
           | <VarName> "=" <Expression> ";" <DefList>

まあ、見た目通りのラムダ計算です。例えば、\s z -> s (s z)はチャーチエンコーディングされた自然数2です。

意味論を細かく定義するのは面倒なので適当に言うなら、ラムダ計算＋letrecで、全部遅延評価します。

また、入出力はLazyK~~をパクった~~と同じ規約を使って行います。すなわち、次のように定めます。

プログラムは入力を引数にとって出力を返す関数である。
入力、出力ともにチャーチエンコーディングされた自然数の、スコットエンコーディングされた無限リストで表す。すなわち次のstreamと同じ形式の関数を用いる。
```
stream = \f0 -> f0 e0 (\f1 -> f1 e1 (\f2 -> f2 e2 (\f3 -> ... )))
    where e0, e1, e2, ... はチャーチエンコーディングされた自然数
```
無限リストの要素は符号なしの1バイト(0…255)を表す。256以上の要素はEOFを意味するものとする。

例をあげると、

入力をそのまま返す恒等関数 \x -> x は、入力をそのまま出力するプログラムです。
入力を無視して常に256の無限リストを返す次の関数は、何も出力せずに終了するプログラムです。
```
letrec { r = \f -> f 256 r } in \x -> r
```
次の関数は、入力の各バイトを2回づつ順に出力するプログラムです。例えば、入力 “abc” に対して “aabbcc” と出力します。
```
letrec {
  pair = \x -> \y -> \f -> f x y;
  go = \xs -> xs (\x xs' -> pair x (pair x (go xs')))
} in go
```

画像から中間言語への翻訳

LambdaBoxのプログラムは、ビットマップ画像として書きます。この画像フォーマットは、各チャネル8ビット深度のRGB画像への変換が一意に定まるなら、何でもいいものとします。

現時点での実装では、使っているライブラリ(JuicyPixels)が.png, .bmp, .jpeg, .gif, .tga, .hdr, .tiffをサポートしているので、これらのフォーマットで24ビットRGBを超えない深度ならOKです。

中間言語への変換は次の手順に沿って行います。

画像の前処理として、黒(#000000)かそれ以外かの2値画像に変換します。
画像を線(Line)の集合に変換します。
線(Line)の集合を箱(Box)とワイヤ(Wire)の集合に分割します。
箱(Box)とワイヤ(Wire)の集合を中間言語に変換します。
不正なプログラムになっていないかチェックします。

前処理は書いてあるそのままなので、次節より2.から順に解説します。

画像を線(Line)の集合に変換

線(Line)は、ここでは、「垂直または水平に2個以上連続した黒のピクセル」と定義します。この処理では、画像を、それに含まれるすべての線の集まりに変換します。このとき、可能な限り長い連続したピクセルを1つの線にまとめます。例えば、 6個まで連続した黒のピクセルは、一本の長さ6の線です。

__######__
  <---->

次のようには複数本には数えません。

__######__
  <-><->

次の画像は5本の線の集合で表されます。

線(Line)の集合を箱(Box)とワイヤ(Wire)の集合に分割

2つの線がどちらかの端点で接している場合、それらの線を接続されているとみなします。2つの線が交差している場合は、接続されていないものとします。

これらの線のうち、4本の線が互いに端点で接して四角形を構成しているものを、箱(Box)とします。

箱に使われなかった線の間の接続関係をグラフとして見たうえで、このグラフの連結成分に分割します。その各連結成分がワイヤ(Wire)になります。ただし、3本以上の線からなるループを含むワイヤがあってはいけません。

次の画像は2本のワイヤから構成されています。交差している線は接続されていないことに注意です。

また、次の画像は2本のワイヤと2個の箱から構成されています。

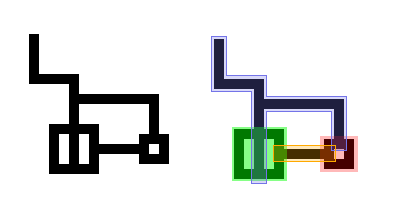
箱とワイヤの集合を中間言語へ変換する

まず、各箱と各ワイヤに、一意な識別子を割り振ります。

次に、各箱を、その入れ子関係がなす木にします。詳しく述べると、

ある箱Aが別の箱Bを完全に含んでいて、包含関係でAとBの間に入る別の箱が存在しなければ、 AはBの親ノードである。
他のすべての箱を完全に含む箱がある。これは木の根ノードになる。
交わっているが、どちらかがどちらかを完全に含むという関係にない2つの箱があってはならない。

という規則で木を作ります。

最後に、根ノードから再帰的に、次のアルゴリズムで中間言語に変換します。

あるノードの箱のサイズが3x3であれば、そのノードは関数適用を表す。
- ノード自体の識別子をboxid
- その箱の左辺に接続しているワイヤの識別子をfun
- 上辺に接続しているワイヤーの識別子をarg
- 下辺と右辺に接続しているワイヤーの識別子をr1, r2
であるとき、この箱は変数定義の集まり、構文で言えば<DefList>として次のように変換される。
```
t_boxid = x_fun x_arg;
x_r1 = t_boxid;
x_r2 = t_boxid;
```
あるノードの箱のサイズが3x3より大きければ、そのノードは関数抽象を表す。
- ノード自体の識別子をboxid
- 上辺に箱の内側から接続しているワイヤの識別子をarg
- 下辺に箱の内側から接続しているワイヤーの識別子をret
- 箱の外側から接続しているワイヤーの識別子をr1, r2, …
- それ以外の方法で接続しているワイヤーはないものとする。
であるとき、この箱は<DefList>として次のように変換される。
```
t_boxid = \x_boxid ->
  letrec {
     arg = x_boxid;
     (すべての子ノードの変換結果);
  } in x_ret;
x_r1 = t_boxid;
x_r2 = t_boxid;
  :
```
ルートノードの識別子をtoplevelとすると、プログラム全体は次のように変換される。
```
letrec {
  (ルートノードの変換結果);
} in t_toplevel
```

例えば、次の画像は2つの箱と2つのワイヤからなります。

それぞれ

外側の箱: 1
内側の箱: 2
上部のワイヤ: 3
下部のワイヤ: 4

と番号を振ると、規則通り変換すれば次のようになります。

letrec {
  t_1 = \x_1 ->
    letrec {
      x_3 = x_1;
      t_2 = \x_2 ->
        letrec {
        } in x_3;
      x_4 = t_2;
    } in x_4;
} in t_1

見た目は複雑ですが、整理すると、\x_1 x_2 -> x_1という簡単な関数だったことがわかります。

不正なプログラムのチェック

ここまでの手順を終えてできた中間言語は、正しくないことがあります。たとえば、定義されていない変数を使っていたり、変数がそのスコープを超えて使われていることがあります。こうしたエラーがないことを確認すると、晴れて中間言語への変換完了です。